Phase Retrieval for Fourier Ptychography under varying amount of measurement

In BMVC 2018 [paper] [code]

Lokesh Boominathan, Mayug Manipirambil, Honey Gupta, Rahul Baburajan, Kaushik Mitra

Abstract

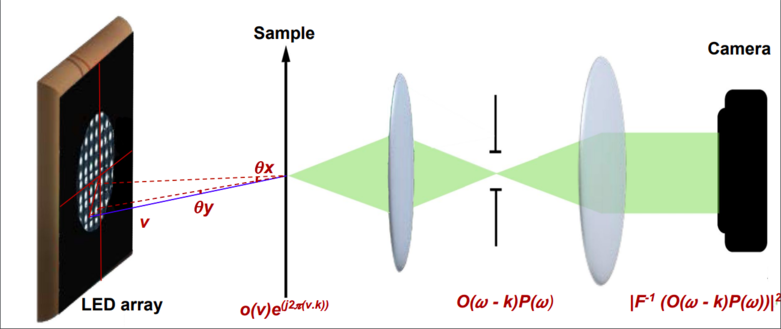
Fourier Ptychography is a recently proposed imaging technique that yields high-resolution images by computationally transcending the diffraction blur of an optical system. At the crux of this method is the phase retrieval algorithm, which is used for computationally stitching together low-resolution images taken under varying illumination angles of a coherent light source. However, the traditional iterative phase retrieval technique relies heavily on the initialization and also need a good amount of overlap in the Fourier domain for the successively captured low-resolution images, thus increasing the acquisition time and data. We show that an auto-encoder based architecture can be adaptively trained for phase retrieval under both low overlap, where traditional techniques completely fail, and at higher levels of overlap. For the low overlap case we show that a supervised deep learning technique using an autoencoder generator is a good choice for solving the Fourier ptychography problem. And for the high overlap case, we show that optimizing the generator for reducing the forward model error is an appropriate choice. Using simulations for the challenging case of uncorrelated phase and amplitude, we show that our method outperforms many of the previously proposed Fourier ptychography phase retrieval techniques.

Fourier Ptychography Forward Model

• LED illumination: Let us consider the imaging of a thin target sample having transmission function given by $o(v)=A(v)\mathrm{e}^{j\phi(v)}$, where $v$ is the spatial vector, and $A(v)$ and $\phi(v)$ are the amplitude and phase attenuation respectively. If the target sample is illuminated using an LED that emits light with spatial frequency $k$, then light from the target sample that reaches the objective lens is $o(v)\mathrm{e}^{j2\pi(v.k)}$. Therefore, if $O(\omega)$ is Fourier transform of the target sample under normal illumination, then the Fourier transform under angular illumination would be $O(\omega-k)$.
• Objective lens: Let $P(\omega)$ be the pupil function of the objective lens, then the light passing through it would be $O(\omega-k)P(\omega)$. Since under normal illumination $P(\omega)$ acts as a low pass filter with cut-off frequency given by its numerical aperture, under angular illumination it would behave as a band pass filter.
• Image acquisition: However, since camera sensors can capture only the intensity and not the phase of light coming from the objective lens, the captured image is given as $|{\mathcal{F}}^{-1}(O(\omega-k)P(\omega))|^2$, where ${\mathcal{F}}^{-1}$ is Fourier inverse. Multiple such images are taken using varying angles of illumination to capture different regions of the object's Fouier domain.

Our Contribution

We show that an auto-encoder based architecture can be adapted for performing FP phase retrieval under varying levels of overlap. We do this by using the same generator network, but different optimization frameworks depending on the amount of overlap. For low overlap case, due to lack of sufficient measurements, we resort to a supervised learning based technique that learns a conditional prior to map the low resolution measurements to its high resolution phase and amplitude.For higher overlap, we propose a non-data driven framework, where we optimize over the generator parameters by minimizing the forward measurement error of FP. While other traditional algorithms also optimize in a similar way, the proposed method additionally exploits the low-level image statistics captured by generator network’s inherent structure, thereby making it more robust to phase-amplitude leakage.Using simulations for uncorrelated phase and amplitude in both low and high overlaps, we show that our algorithm outperforms previously proposed FP phase retrieval.

Method

For the low overlap case (0% and 15%), where the number of measurements are significantly lower than the number of unknowns, we take a supervised learning approach. Using a training dataset, We learn a conditional prior for mapping the low resolution images to its high resolution phase and amplitude images. In case of higher overlap (40% and 65%), we propose a non data-driven deep learning technique that directly exploits the measurement constraints. This involves adding the forward model to the generator network, so as to compute the loss between observed and estimated low resolution measurements. We show that even randomly initializing the generator network, and then optimizing its weights for a given set of test measurements can reconstruct the high resolution amplitude and phase. Such a framework also exploits the additional natural image prior induced by the structure of generator network [29], making it more robust to phase-amplitude leakage.

Methods in the comparison

• RW Gerchberg. Super-resolution through error energy reduction. Optica Acta: International Journal of Optics, 21(9):709–720, 1974.
• James R Fienup. Reconstruction of an object from the modulus of its fourier transform. Optics letters, 3(1):27–29, 1978.
• Armin Kappeler, Sushobhan Ghosh, Jason Holloway, Oliver Cossairt, and Aggelos Katsaggelos. Ptychnet: Cnn based fourier ptychography. In Image Processing (ICIP), 2017 IEEE International Conference on, pages 1712–1716. IEEE, 2017.

Publications

1. Lokesh Boominathan, Mayug Maniparambil, Honey Gupta, Rahul Baburajan, Kaushik Mitra, "Phase retrieval for Fourier Ptychography under varying amount of measurements", accepted at BMVC, 2018